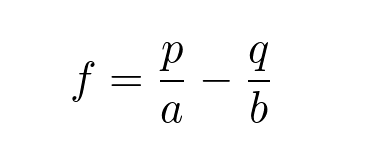Welcome to the 14 new investors joining us since last Monday. If you’re reading this, but haven’t subscribed, join our family of 695 smart, growth-mindset folks here!
If you enjoy or get value from Investing Lessons, consider helping me reach 1,000 subscribers by the end of June (my birthday!) by doing any of the following:
Forwarding this post to friends, and getting them to subscribe.
Sharing on Twitter, Facebook, and Linkedin with a note of what you learned.
Sharing within community or company Discord/Slack/Facebook groups.
Let’s play a game.
Suppose you have $100. You are to flip a coin 100 times. For each flip, heads will double your bet and tails will halve your bet.
Should you take this bet?
Expected Payoff
As discussed previously in “Are you trading or gambling?”, you should only take a bet if it has a positive expected payoff. Let us crunch the numbers to see what will happen.
For the first flip, let us assume you bet $100. You have a 50% chance of winning $100, but also a 50% chance of losing $50. On average, you will gain ($100 + -$50)/2 = $25 or 25% with that bet. While the amount you bet may change with every flip, you are still expected to gain 25%.
Should you take this bet?
Losing Money on Positive Expected Value Bets?!
A powerful technique in grasping intuition for difficult problems is to consider extreme cases. Here, let us simplify the problem by betting everything you have with each coin flip.
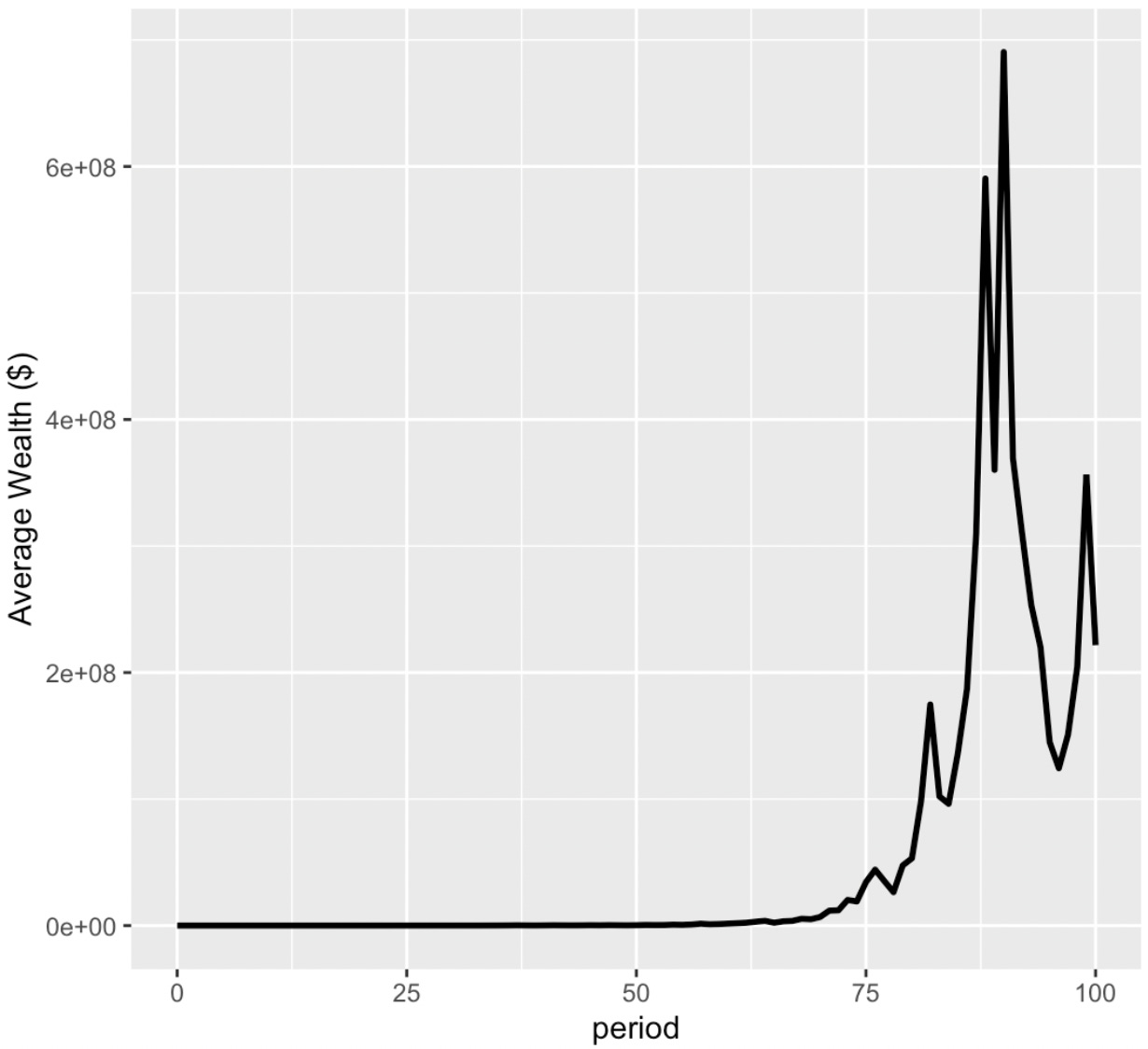
Let us simulate a population of 1000 people, each starting with $100 and flipping the coin 100 times. At first glance it appears that the average wealth of the population is increasing, consistent with our theory of positive expected payoffs.
However if we look closer, we see something interesting. While the average wealth is increasing as expected to over $200M, the median wealth is actually less than $100. In fact, over 25% of people have lost over 99% of their wealth!
For most people, taking the bet is a disaster. The returns only look good on average, as it is propped up by the large asymmetric returns of a few lucky individuals. Here the expected positive payoff does not match the actual experience.
The notion of losing money on positive expected value bets is quite counterintuitive.
The Kelly Criterion
The above experiment begs the following question: “How can one make positive value bets, in a way that maximises returns?”
Luckily in 1956, John Kelly developed his Kelly Criterion with Claude Shannon, a formula for bet sizing that maximises returns in the long run.
Legend has it that Shannon went to Las Vegas to test this idea out with Ed Thorp, making a fortune in the process of playing games they had a positive edge in. This dynamic pair of mathematicians helped pioneer the statistical arbitrage strategy, which made annualised 20% returns over an (almost) 30 year span.
The Kelly Criterion formula for a bet is as follows:
where
f is the fraction of the current bankroll to invest
b is the amount you potentially gain in your bet or investment
a is the amount you potentially lose in your bet or investment
p is the probability of winning
q is the probability of losing
When applied to our game, a = 1 and b = 0.5, suggesting that the optimal bet size should be 50% of your current bankroll. This means that for our first bet, we should wager $50. Subsequent bets are then adjusted accordingly based on our new bankroll.
Practical Considerations
Kelly Criterion is used widely by professional investors, traders, and gamblers.
For instance, bet sizing of hands is an important concept in poker theory. For those interested, check out Bill Chen’s book on “The Mathematics of Poker”. He is a WSOP Bracelet Winner and Quantitative Researcher at SIG.
In most practical instances, the true odds and payoff profiles are unknown. By using historical data as a guidance, investors or traders are able to grasp a rough idea of what these inputs should be. This is unlike games with explicit payoffs such as Blackjack games,
Another consideration practically is the concept of ‘risk of ruin’. This is the likelihood that one's entire bankroll is extinguished, meaning that they are unable to make any subsequent bets. It does not matter how favourable an investment is, if one cannot pony up cash.
The combination of these two practicalities requires the practitioner to be more prudent than what the original Kelly Criterion suggests. This resulted in the popularisation of running fractional Kelly bets such as half Kelly, where one bets half of the full Kelly bet size.


Other Posts on Betting, Trading, and Gambling
Are you trading or gambling? How to not be a degenerate trader.
Should you buy a ‘lottery ticket’? Making positive value bets with asymmetric payoffs.
Is the bull case for Bitcoin really $1,000,000?
Understanding why you need Insurance - the only negative value you should take!