Should You Buy a Lottery Ticket?
Seeking Positive EV Bets with Asymmetric Payoffs: $65 into $12,000
If you enjoy or get value from Investing Lessons, consider helping me reach 1,000 subscribers by the end of June (my birthday!) by doing any of the following:
Forwarding this post to friends, and getting them to subscribe.
Sharing on Twitter, Facebook, and Linkedin with a note of what you learned.
Sharing within community or company Discord/Slack/Facebook groups.
You might have heard that purchasing lottery tickets is a bad idea, and that you are almost certainly going to lose money on it. However just because it gives you an improbable chance of hitting the jackpot, doesn’t mean it is a mistake.
If it was, then purchasing insurance would be a bad decision given how infrequent claim events occur. Purchasing home insurance is quite literally the definition of betting for your house to burn down, so that you win a large payout. [1]
Positive Expected Value Bets
In the previous post regarding trading vs gambling, we brushed upon the notion of making positive expected value (EV) bets. To reiterate, these are bets made such that you will make money in the long run.
This is important.
What makes lottery tickets bad, is the fact that it is a negative EV bet. This means that you are effectively throwing away money with every ticket you purchase - this is no different than testing your luck at a slot machine (or pokies). Sure, you might get lucky in the short term - but the odds of you being struck by lightning are higher than you winning.
Asymmetric Payoff Bets
You might be thinking now if there exists such a bet where you could potentially win big time, and yet is a positive EV bet. And the answer to this, is that it certainly exists - but it is rare. Most Wall Street trading firms purchase volatility cheaply and in the event of a market crash, these payout hundred-fold. Jane Street made $8 Trillion in the 2020 crash essentially from this.
However before you go and hastily punt on volatility, such strategies are generally reserved for large institutions. These are often treated as a cost of doing business, and typically result in worthless payouts. More on volatility in future newsletters, but a good proxy of thinking about it is how much someone would pay for insurance (obviously more if they are scared).
Case Study
So where else might you find such opportunities? While I generally do not condone blindly trading options, it does give us a great case study to a great trade (in my opinion).
Unless you have been living under a rock for the last few weeks, you would have heard about the Gamestop (GME) short-squeeze. The short-squeeze sent the price of GME hurdling from about $35 a share, to record highs of $483. The price then came crashing down back to about $40 after Robinhood and other brokers disabled the buy button.
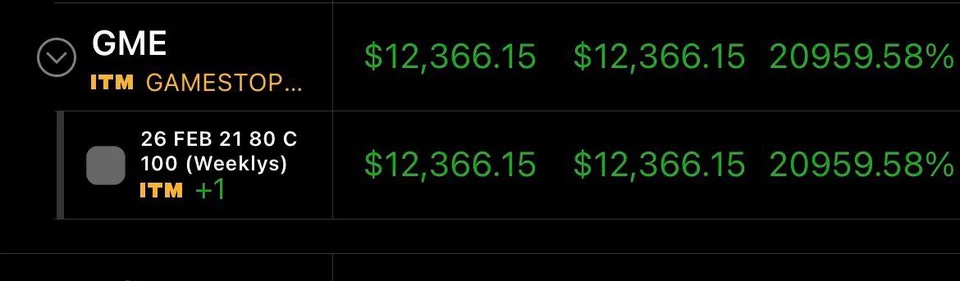
Below is the screenshot of an individual on r/wallstreetbets who posted a 20,000% gain, where he turned one call option worth $65 into $12,000. To the skeptics, our first reaction to this trade is that of luck placed by a degenerate gambler. However this trade certainly did possess the hallmarks of a positive EV trade with asymmetric payoffs, with good bet sizing (max loss $65).
The obvious discussion here is whether or not it was a positive EV trade. Given the extremely thinly traded float, coupled with several hedge funds doubling down their short positions, it stands that there is a non-zero probability that GME experiences at least a tiny second short squeeze to perhaps $100.
In a simplified scenario, let us consider that if GME reaches $100, then we win $12,000; otherwise it is worth nothing and we lose $65. A good question to ask here is - what are the implied odds? To rephrase this in plain english, what must be the probability such that this bet is a positive EV bet? The answer is 0.5%. [2]
If you believe the chance of a second short squeeze happening is greater than 0.5%, then you certainly should place this bet. You can think of probabilities much like dollars. If something is selling for $0.50, but you think it is worth $2.00 - then you should certainly buy it!
Look out for positive EV bets with asymmetric upside!
[1] Some readers wrote in and mentioned that insurance is a negative EV bet, given that insurance firms need to make a profit. So why do we take out insurance then? Sometimes it is worth making a negative EV bet not as a trade, but an expense, in order to ensure that you are not wiped out by some catastrophic event. This is why I mentioned that Jane Street treats some of its tail-event insurance options as an expense.
[2] The mathematics for this is as follows. Assume that the probability of GME reaching $100 or beyond is p. Therefore 12,000 * p + (-65) * (1 - p) = 0. Rearranging the formula gives us a p value of 0.5%.