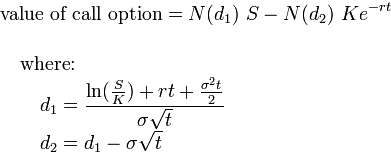How Black Scholes Precipitated the 1987 Black Monday Financial Crash
Options Trading: The Untold Story (Pt2)
Welcome to the 17 new investors joining us since last Monday. If you’re reading this, but haven’t subscribed, join our family of 492 smart, growth-mindset folks by subscribing here!
If you enjoy or get value from Investing Lessons, consider helping me reach 1,000 subscribers by the end of June (my birthday!) by doing any of the following:
Forwarding this post to friends, and getting them to subscribe.
Sharing on Twitter, Facebook, and Linkedin with a note of what you learned.
Sharing within community or company Discord/Slack/Facebook groups.
Options Trading: The Untold Story
Part 1 - The Humble Greek Origins of Options Trading
Part 2 - How Black Scholes Precipitated the 1987 Black Monday
Part 3 - How Abusing Derivative Correlations Caused the 2008 GFC
Buckle up!
This is the second of a three-part series. Today, you will learn about how abusing a Nobel Prize-winning formula, paired with the rise of electronic trading, led to a $1.7 trillion global-market crash on the dawn of October 19th, 1987…
The First Practical Book on Options Trading
The Black Scholes model was revered due to its immense power, yet being remarkably simplistic. It was a simple formula that could calculate the theoretical price of an option at any moment in time by just knowing the current stock price.
Although options contracts were being traded as far back as the Ancient Greeks, there never was a way to calculate its value! Writers of these contracts had to essentially ballpark its value based on rough mathematics and experience.
This was a problem.
As the financial sector grew in size, becoming more and more sophisticated, there was a real need for a more precise way of pricing options. Entire multi-million businesses were now on the line, rather than the paltry olive-presses of the Ancient Greeks.
Some savvy traders took note of the blatant mispricings in the market. In 1877, Charles Castelli published one of the first books on options trading, detailing arbitrage opportunities in his “Theory of Options in Stocks and Shares”.
While the book delivered little theoretical basis, it did shed practical insight on how to profit off significant mispricings or arbitrages. Included is a crazy intercontinental options trade between London and Constantinople (Turkey) rooted in deviations from the put-call parity.
Already, you can see the existence of major market inefficiencies at play.
The Origin Story of the Black Scholes Model
Twenty-three years later in 1900, a graduate student by the name of Louis Bachelier published his thesis paper “The Theory of Speculation”.
Bachelier created the first complete mathematical model of options trading. He compares the random fluctuations of the market to the random movements of particles suspended in fluids - also known as Brownian Motion.
Remarkably, the Brownian Motion described in this paper not only became the foundation in the Black Scholes model, but also anticipates key insights later developed by Albert Einstein.
Unfortunately, the model contained financially unrealistic assumptions such as the stock price becoming negative. Other researchers tried as well for the better half of the 19th century, but their efforts were also fruitless. The models developed were overly complicated, and contained parameters that could not be measured.
Then in 1968, the heros of our story enter. Independent finance contractor, Fisher Black, and MIT assistant professor of finance, Myron Scholes, joined forces to begin their work on options pricing. They wanted a simple formula that could calculate the fair price of an option, at any moment in time by simply knowing the stock price.
Rather than building upon the complex equations of their predecessors, Black and Scholes stripped the previous formulas to its bare-boned states - reasoning by first principles if you will. They also removed all parameters that were unmeasurable.
Ingredients for the Black Scholes Model
By the time they were done, they were left with five key parameter inputs of the modern Black Scholes model:
Underlying asset price
Strike price
Time to expiry
Interest rate
Volatility
All five parameters are measurable, with only volatility being not capable of being explicitly observed. Volatility is the measure of how much a stock deviates from its expected movement. The problem with volatility is that it can only be measured retrospectively, after the fact.
To resolve the problem of volatility being unmeasurable, they figured they could make the parameter less significant. The solution to this, was the concept of risk-neutral pricing through dynamic hedging. If this sounds complicated, let us break it down.
The concept of hedging came from the world of gambling. When one makes a bet, they could also hedge their bet by also betting in the opposite direction. Hedging is not only found in gambling, but also businesses.
Suppose you own an airline business. You are constantly in need for fuel, but want to protect yourself from rising fuel prices that erodes your margins. So you decide to hedge your business by buying an oil refinery, which will minimise your risk at the cost of lowering your potential gains.
Black and Scholes realised they were able to replicate any options position with a theoretical portfolio of stock and cash (without arbitrage of course!). Using this idea, they were able to hedge an option in a way that cancelled out any market movement - this is now known as being delta neutral. This achievement allowed one to minimise one of the primary sources of risk, delta risk (more on the Greek risks later).
However, there was a practical problem with their formula.
Their current formula assumed that markets were always in equilibrium, but obviously the stock price is in constant flux. They needed a way to instantly rebalance, or dynamically hedge the option to counteract all price movements.
The efforts of Merton and Scholes were rewarded with the Nobel prize in economics in 1997. Black did not end up receiving the award due to passing away in 1994, as Nobel prizes are not awarded posthumously.
Limitations and Abuse of the Black Scholes Model
The Chicago Options Exchange launched in 1973, one month before the Black-Scholes model was published. Traders began using their ideas immediately, causing the options market to explode in volume. Everyone marvelled at the formula’s power, despite its simplistic nature.
Like with all models, Black Scholes had its own limitations.
Its misuse by market participants was a contributing factor to market crashes including the 1987 Black Monday. Black Scholes was grounded in randomness, so it was incapable of predicting the future with 100% accuracy. The financial markets aren’t governed by the Newtonian physical Laws, where outcomes are explicit.
Furthermore there is a danger to blindly accepting the Black Scholes model as truth, as there are important model limitations. In all successful hedge funds, it is treated as a tool for decision making, rather than a source of truth.
We will conclude part 2 by discussing the limitations of the model through the lens of heroic trades and catastrophic implosions by market participants.
How the Volatility Smile Contributed to the 1987 Black Monday Crash
In practice, an option’s theoretical value can be used to infer the volatility by back-solving the Black Scholes model while keeping other parameters constant. This inferred volatility is also known as the implied volatility.
The implied volatility is simply the trader’s best guess as to what the actual volatility is going to be. Remember that volatility can only be calculated retrospectively, so traders are constantly comparing implied vs actual volatility to see if they overpaid or underpaid for an option.
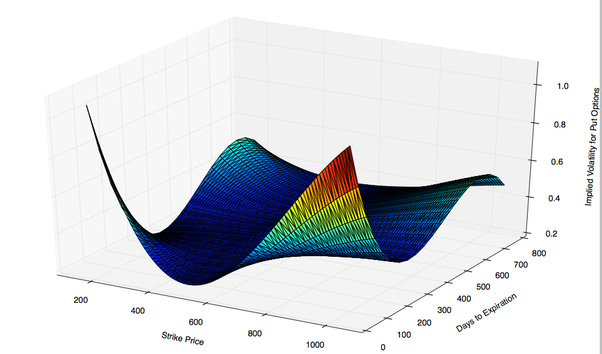
The comparison of implied volatility to options of other strikes and expiry dates allows for the construction of the implied volatility surface. Given that an option’s theoretical value monotonically increases with volatility, traders often price options in terms of implied volatility to spot mispricing opportunities.
The original Black Scholes model assumed constant volatility and log-normal price distributions. However in reality, empirical asset return distributions exhibit fatter tails due to market crashes being more common and significant than otherwise assumed in the model.
While no-one is sure what exactly caused the 1987 Black Monday crash, it did cause a significant change in the markets. One such change, is the market showing the presence of a volatility smile - something not present in the Black Scholes model.
The volatility smile basically is the notion that when you graph implied volatility against the strike price, it creates a smile-like curve where the implied volatility is lower ATM.
The original model had assumed for a constant volatility, but this was not the case due to erroneous tail assumptions. Volatility smiles are not a consequence of Black Scholes theory, but rather a market phenomenon informing us that the assumptions of the model do not hold true under all circumstances.
Note: It is also worth noting is that market practitioners today generally use the term implied-volatility to indicate the volatility parameter for the ATM option.
Many hedge funds got wiped out in the 1987 crash for selling OTM puts, thinking that it was free money given the small probability of a loss. What they were actually doing was described by Nassim Taleb, as “picking up pennies in front of a steamroller”.
Firms that understood the limitations of the Black Scholes model were able to purchase OTM puts cheaply. One such story was the birth of arguably the largest options market-maker in the world, Susquehanna International Group headed by legendary trader Jeff Yass. It is reported that during the crash, they made $30 million off this strategy ($70M today after inflation).
Most sophisticated hedge funds these days counter this flaw in the model by purchasing a warchest of OTM options for insurance against catastrophic bankruptcy.
This hedges against inaccuracies in the model, allowing these firms to maintain solvency during a crisis. Much of Jane Street’s $6.3 billion profits in the first half of 2020 and Citadel’s $6.7 billion profits for the entirety of 2020 can be attributed to this.
How the Black Scholes Model Contributed to... More Market Crashes
Just when you thought the volatility smile was the only mishap in the Black Scholes model, enter the volatility skew.
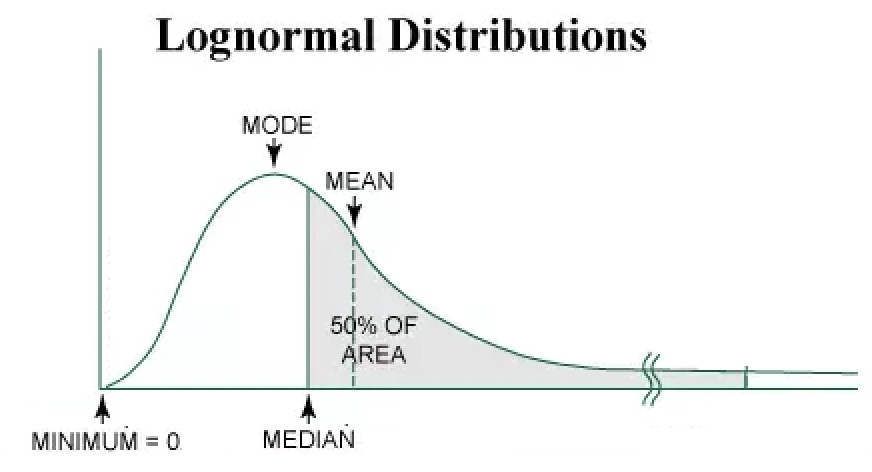
Recall that the Black Scholes model assumed a log-normal distribution in stock returns. For those unfamiliar with statistics, it is as the name suggests - quite literally the logarithm of a normal distribution. This ensures that the stock price can never be negative, while suggesting that extreme moves are less likely as the stock’s price approaches zero.
One easy way to spot a flaw in this assumption is to look at the mean in relation to the median.
Recall that the median is the middle number. So in frequentist probability terms, the returns in the area to the right of the median has a 50% chance of occurring.
Now recall that the mean is the average. So the mean can be thought of as the expected return. As option prices are priced on expected returns, actual realised returns greater than the mean will be a profit or positive PnL, and vice versa.
As the median is less than the mean in a log-normal distribution, this implies that a trade is profitable less than 50% of the time. We can see from empirical data that this is clearly wrong, as simply holding an ETF long-term guarantees profit. Furthermore, this implies that every trade is likely negative expected value, resulting in zero trades from any rational market participant.
In order for the distribution to be consistent with empirical evidence, the median needed to be greater than the mean. To achieve this, the log-normal function was skewed mathematically. This resulted in the birth of the volatility skew, where the OTM put options carry a higher premium than its counterpart OTM call option.
Insider reports from Susquehanna employees reports that the firm made several billion dollars in profit during the 2000 Dot Com Crash from buying volatility skew cheaply (again). While volatility smiles were now prevalent knowledge, traders were still underpricing the OTM puts that were being sold to them.
Practical Ways to Trade Volatility
To wrap things up, modern option traders can bet on volatility in two major ways.
The entire implied volatility surface moving upwards or downwards, such as in the case of market crashes. Volatility is typically mean-reverting, and so traders use historical data to decide which direction to bet on. Usually though, most hedge funds want to be buying volatility (by purchasing any option).
The implied volatility surface can steepen or flatten, depending on market impact ITM and OTM. This presents skew trades, as the implied volatility see-saws too far in one particular direction.
Next week will conclude this three-part series on the history of options. We will look at how mispricing (again!) correlations between different derivatives, led to the Global Financial Crisis…
Market Musings
Here is a hypothetical trade:
You purchase some useless cryptocurrency as a joke, for about $0
The price of this meme altcoin goes to the moon, so it is now worth $1,000,000
If you tried to sell it, you would crash the market. You might be lucky to escape with $500,000 dollars - not bad.
Assuming a 30% capital-gains tax rate, you would end up with $350,000
Let us suppose you have a $1,500,000 income, being taxed at 45%.
If you donate it to charity, you end up with a $1,000,000 taxable deduction, that will cut your tax bill by $450,000
Donating to charity makes you $100,000 more than selling it
This scenario occurred when Vitalik Buterin, co-founder of Ethereum, decided to donate a billion dollars worth of Shiba Inu coin to some Covid-19 relief charity.